머피의 법칙에도
과학이 숨어 있다

우리는 일상 속에서 종종 설명하지 못할 불행한 순간들을 겪고는 합니다. 왜 꼭 내가 지각하는 순간에만 신호등이 걸리는 것인지, 왜 꼭 토스트는 버터를 바른 쪽이 바닥을 향해 떨어지는 것인지, 왜 마트에서는 내가 서 있는 줄만 줄어들지 않는 것인지 등, 이러한 불합리한 상황들은 불행이 모두 나에게만 일어나는 것 같다는 말도 안 되는 착각에 빠지게 만듭니다.
이렇게 우연인 듯 우연 아닌 것만 같은 불행한 상황에 대해 처음으로 정의를 내린 한 사람이 있었습니다. 그는 1949년, 미 공군 소속 대위였던 에드워드 머피였습니다. 에드워드 머피는 미 공군의 음속기 개발을 위해 인체가 견딜 수 있는 중력의 한계를 연구하고 있었고, 그 과정 중 자신의 부하에게 측정장치를 설치할 것을 명령했습니다. 하지만 부하 기술자들이 머피가 설계한 전극봉을 모두 잘못된 방법으로 조립했다는 것을 알게 되었고, 그 결과 모든 실험값이 0이 나오는 참사가 일어나게 됩니다.

이러한 일이 있고 난 후 머피는 ‘어떤 일을 하는 데는 여러 가지 방법이 있고, 그 가운데 한 가지 방법이 재앙을 초래할 수 있다면 누군가가 꼭 그 방법을 쓴다’라는 법칙을 만들었습니다. 이 법칙이 바로 모두 익히 들어 보았을 그 유명한 ‘머피의 법칙’입니다.

‘머피의 법칙’은 주로 인간의 심리적인 현상을 정의할 때 쓰이는 이론 중 하나인데요, 흥미롭게도 심리적 현상으로만 여겨졌던 ‘머피의 법칙’의 사례들을 과학적으로 증명해낸 학자들이 있다고 합니다. ‘왜 토스트는 꼭 버터를 바른 쪽이 바닥을 향해 떨어지는 것인가?’

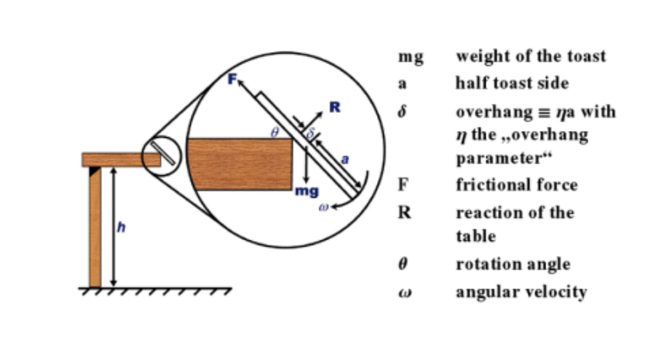
영국 애슈턴 대학 정보공학과에서 연구원으로 일하고 있는 로버트 매튜스는 우리의 이러한 일상 속 딜레마를 과학적으로 증명하며 큰 주목을 받았습니다. 그는 처음으로 버터 바른 토스트가 바닥을 향해 떨어지는 이유를 논리적으로 설명한 과학자이기도 합니다. 로버트 매튜스는 먼저 사람들이 토스트를 식탁에서 떨어뜨리거나 들고 있다가 떨어뜨리는 경우를 가정하였어요. 그는 버터를 바른 쪽이 위로 향한 토스트가 식탁에서 떨어지는 경우, 두 면 중 어떤 면이 바닥으로 떨어질 것인가를 결정하는 문제는 토스트를 회전시키는 스핀이 결정한다고 보았습니다.
이 스핀의 힘을 물리학자들은 ‘토크’라고 부릅니다. 그리고 이러한 경우에서 중력이 토크의 역할을 수행하게 되지요. 그는 평균적인 테이블의 높이와 사람들의 키, 토스트의 크기, 지구의 중력 가속도 등을 모두 고려해 계산했을 때 토스트가 떨어질 때 토스트는 한 바퀴의 회전을 채우지 못한다고 주장했습니다. 토스트가 한 바퀴를 회전할 만큼 지구의 중력이 강하지 않다는 것을 이야기한 셈입니다.
이러한 결과에 따라, 토스트는 항상 반 바퀴 정도 회전한 후 착지하기 때문에 버터를 바른 면이 위쪽을 향한 채로 놓여있는 토스트는 거의 필연적으로 반 바퀴를 돈 채 버터 바른 면이 바닥을 향해 떨어질 수밖에 없다고 증명해냅니다. 즉, 이 문제를 물리적으로 계산해 보았을 때 공기의 저항과 토스트에 묻힌 버터의 무게는 토스트 회전에 거의 영향을 미치지 않고 결국 버터 바른 면이 바닥을 향해 떨어진다는 결과는 지구의 중력과 식탁의 마찰계수가 변하지 않는 한 필연적인 결과로 작용하는 것입니다.
왜 내 계산대의 줄은 가장 늦게 줄어드는 것인가?’

로버트 매튜스는 ‘버터 바른 토스트’ 뿐만 아니라 다른 사례들도 차례로 증명해냈습니다. 그중에서도 가장 유명한 ‘계산대 문제’는 많은 사람들의 간지러운 부분을 속 시원하게 해결해준 증명이기도 합니다.
그는 마트에 세 개의 계산대가 있다고 가정한 후, 그중 하나의 계산대에 자신이 줄을 설 것이고 그러므로 자신이 서지 않은 계산대는 두 개가 남을 것이라고 가정하였습니다. 이러한 상황에서 자신이 선 계산대의 줄이 가장 빨리 줄어들 확률은 1/3이 됩니다. 자연스럽게 자신이 서지 않은 계산대의 줄이 가장 빨리 줄어들 확률은 2/3가 됩니다. 이는 약 2배의 차이가 나게 되지요. 또한, 대형마트 같이 손님이 많은 곳은 그 계산대의 숫자도 3개를 넘어 점점 더 많아지기 때문에 이러한 결과값은 차이가 계속해서 더 크게 벌어질 수밖에 없습니다.
예를 들어, 계산대의 개수가 n이라면 자신이 선 곳의 줄이 가장 빨리 줄어들 확률은 n분의 1이고, 나머지 줄이 가장 빨리 줄어들 확률은 n분의 1이기 때문에 다른 줄이 가장 빨리 줄어들 확률이 (n-1)/n으로 (n-1)배씩 커지기 때문입니다. 이러한 결과를 바탕으로 로버트 매튜스는 자신이 선 줄이 항상 길다고 느껴지는 것은 지극히 자연스러운 일이라고 분석하였습니다.
이외에도 머피의 법칙은 다양한 사례들로 나타나는데요, 과학자들은 과학적으로 아직 증명되지 않은 다른 사례들에 대해서 이러한 현상이 인간의 ‘선택적 기억’ 때문에 일어난다고 보았습니다. 선택적 기억은 기억이 선택적으로 이루어지는 현상을 말합니다. 더 풀어서 이야기하자면, 우리가 실패할 확률이 적은 일을 할 때 그 일이 수월하게 해결된다면 그것을 당연한 일이라고 뇌가 인식한 후 장기 기억으로 전환하지 않게 됩니다. 하지만 만약에 그 일이 실패하게 된다면 실패한 사건으로 뇌리에 박히게 되는 것입니다. 이러한 상황이 반복되다 보면 성공한 사례보다 기억 속에 축적된 실패한 사례만 머릿속에 남게 되어 모든 일이 실패하는 것처럼 느끼게 되는 것입니다.

우리 모두 인생이 힘들고 막막할 때, ‘왜 나에게만 이런 안 좋은 일이 생기는 것일까’라는 의문이 드는 순간이 있을 것입니다. 하지만 우리의 인생을 돌이켜 잘 살펴본다면 힘든 횟수에 비례하는 만큼 즐겁고 행복했던 경험들도 많이 존재할 것입니다.
‘머피의 법칙’은 결국 안 좋은 일은 내게만 찾아온다는 통상적인 믿음과 다르게 단순한 확률의 문제로 생각될 수 있는 문제들이니까요. ‘결국, 일어날 일은 일어난다.’라는 본질적인 의미를 지닌 ‘머피의 법칙’을 잘 이해하게 된다면 앞으로의 인생을 긍정적으로 바라보는 시야를 얻을 수 있을 것입니다. 행복한 일도 결국 일어나게 될 것이니까 말이지요. 지금껏 자신의 인생이 힘든 일만 가득했다는 생각이 들어도 낙심하지는 마세요. 경우의 수만큼, 그 확률만큼 앞으로는 여러분의 인생에 행복하고 즐거운 일이 가득할 테니까요.
'Semiconductor > 스마트 Tip' 카테고리의 다른 글
| [유쾌한 과학 이야기] 꿈의 신소재 그래핀, 엉뚱함을 기반으로 탄생하다 (0) | 2021.02.18 |
|---|---|
| [디지털 라이프] 돌돌 말았다 폈다, 롤러블에 마음을 뺏겼다! (0) | 2021.02.16 |
| [디지털 라이프] 2021년, 10년 후를 바라보다, 6G 시대가 온다고?! (0) | 2021.01.12 |
| [세계 과학자의 대학] 법대에 간 과학자, 맥스웰과 케임브리지 대학 (0) | 2020.12.22 |
| [디지털 라이프] 2021년 IT 기술, _________ 빈칸에는 어떤 이야기가? (0) | 2020.12.15 |



